The Field Of Statistics Is Doomed — Unless It Abandons Testing & Parameter-Based Analysis
By William Briggs
We already saw a study from Nate Breznau and others in which a great number of social science researchers were given identical data and asked to answer the same question—and in which the answers to that question were all over the map, with about equals numbers answering one thing and others answering its opposite, all answers with varying strengths of association, and with both sides claiming “statistical significance.”
If “statistical significance”, and statistical modeling practices were objective, as they are claimed to be, then all those researchers should have arrived at the same answer, and the same significance. Since they did not agree, something is wrong with either “significance” or objective modeling, or both.
If “statistical significance”, and statistical modeling practices were objective, as they are claimed to be, then all those researchers should have arrived at the same answer, and the same significance. Since they did not agree, something is wrong with either “significance” or objective modeling, or both.
The answer will be: both. Before we come to that, Breznau’s experiment was repeated, this time in ecology.
The paper is “Same data, different analysts: variation in effect sizes due to analytical decisions in ecology and evolutionary biology” by Elliot Gould and a huge number of other authors, from all around the world, and can be found on the pre-print server EcoEvorxiv.
The work followed the same lines as with Breznau. Some 174 teams, with 246 analysts in total, were given two identical datasets and they were asked “to investigate the answers to prespecified research questions.” One dataset was to “compare sibling number and nestling growth” of blue tits (Cyanistes caeruleus), and the other was “to compare grass cover and tree seedling recruitment” in Eucalyptus.
The analysts arrived at 141 different results for the blue tits and 85 for the Eucalyptus.
For the blue tits (with my emphasis):
“For the blue tit analyses, the average effect was convincingly negative, with less growth for nestlings living with more siblings, but there was near continuous variation in effect size from large negative effects to effects near zero, and even effects crossing the traditional threshold of statistical significance in the opposite direction.”
Here’s a picture of all the results, which were standardized (that Zr in the figure) across all entries for easy comparison.
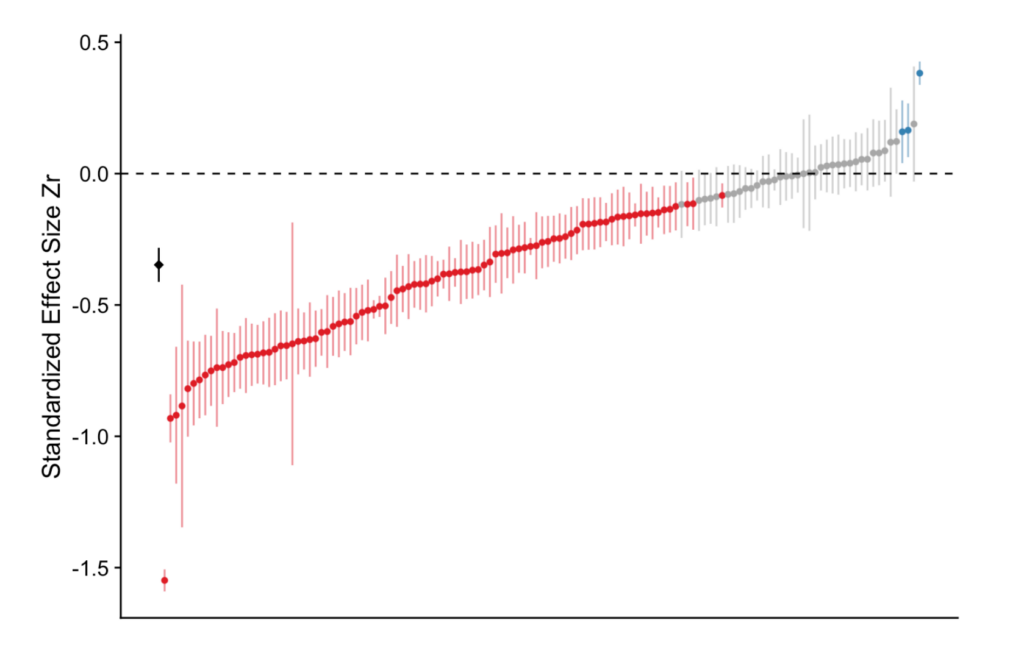
The center of each vertical line is the standardized effect found for each research result, with the vertical lines themselves being a measure of uncertainty of that effect (a “confidence interval”), also given by the researchers. Statistical theory insists most of these vertical lines should overlap on the vertical axis. They do not.
The red dots, as the text indicates, are for negative effects that are “statistically significant”, whereas the blue are for positive, also “significant”.
Now for the Eucalyptus (again my emphasis):
“[T]he average relationship between grass cover and Eucalyptus seedling number was only slightly negative and not convincingly different from zero, and most effects ranged from weakly negative to weakly positive, with about a third of effects crossing the traditional threshold of significance in one direction or the other. However, there were also several striking outliers in the Eucalyptus dataset, with effects far from zero.”
Here’s the similar picture as above:
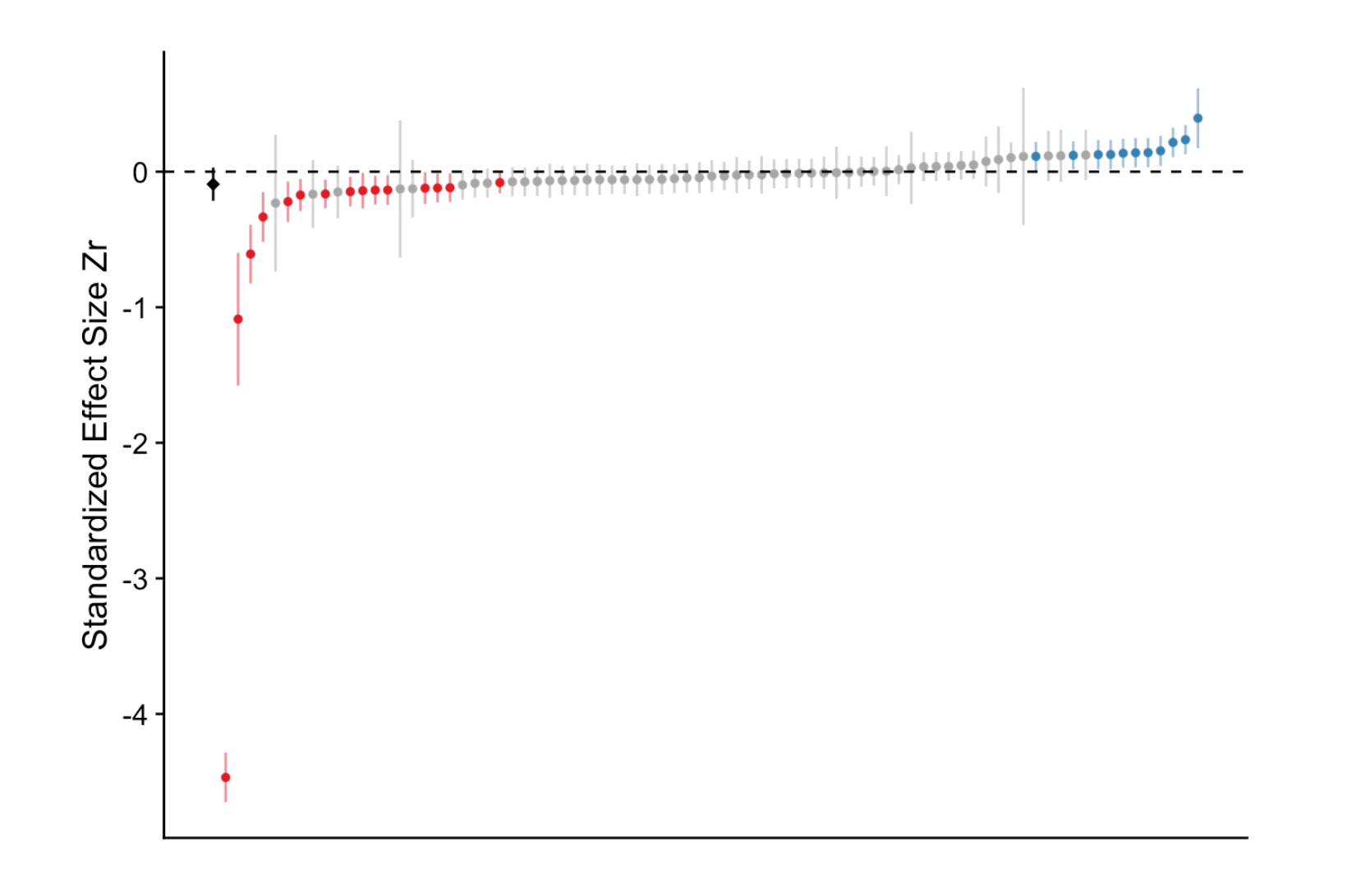
This picture has the same interpretation, but notice the “significant” negative effects are more or less balanced by the “significant” positive effects. With one very large negative effect at the bottom.
If statistical modelling was objective, and if statistical practice and theory worked as advertised, all results should be the same, for both analysis, with only small differences. Yet the differences are many and large, as they were with Breznau; therefore, statistical practice is not objective, and statistical theory is deeply flawed.
There are many niceties in Gould’s paper about how all those analysts carried out their models, with complexities about “fixed” versus “random” effects, “independent” versus “dependent” variables, variable selection and so forth, even out-of-sample predictions, which will be of interest to statisticians. But only to depress them, one hopes, because none of these things made any difference to the outcome that researchers disagreed wildly on simple, well defined analysis questions.
The clever twist with Gould’s paper was that all the analyses were peer reviewed “by at least two other participating analysts; a level of scrutiny consistent with standard pre-publication peer review.” Some analyses came back marked “unpublishable”, other reviewers demanded major or minor revisions, and some said publish-as-is.
Yet the peer-review process, like details about modeling, made no difference either. The disagreements between analysts’ results was the same, regardless of peer-review decision, and regardless of modeling strategies. This is yet more evidence that peer review, as we have claimed many times, is of almost no use and should be abandoned.
If you did not believe Science was Broken, you ought to now. For both Breznau and Gould prove that you must not trust any research that is statistical in nature. This does not mean all research is wrong, but it does mean that there’s an excellent chance that if a study in which you take an interest were to be repeated by different analysts, the results could change, even dramatically. The results could even come back with an opposite conclusion.
If you did not believe Science was Broken, you ought to now. For both Breznau and Gould prove that you must not trust any research that is statistical in nature.
What went wrong? Two things, which are the same problem seen from different angles. I’ll provide the technical details in another place. Or those with some background could benefit from reading my Uncertainty, where studies like the one we discussed today above have been anticipated and discussed.
For us, all we have to know is that the standard scientific practice of model building does not guarantee, or even come close to guaranteeing, truth has been discovered. All the analyses handed in above were based on model fitting and hypothesis testing. And these practices are nowhere near sufficient for good science.
To fix this, statistical practice must abandon its old emphasis on model fitting, with its associated hypothesis testing, and move to making—and verifying—predictions made on data never seen or used in any way. This is the way sciences like Engineering work (when they do).
This is the Predictive Way, a prime focus of Broken Science.
I am a wholly independent writer, statistician, scientist and consultant. Previously a Professor at the Cornell Medical School, a Statistician at DoubleClick in its infancy, a Meteorologist with the National Weather Service, and an Electronic Cryptologist with the US Air Force (the only title I ever cared for was Staff Sergeant Briggs).
My PhD is in Mathematical Statistics: I am now an Uncertainty Philosopher, Epistemologist, Probability Puzzler, and Unmasker of Over-Certainty. My MS is in Atmospheric Physics, and Bachelors is in Meteorology & Math.
Author of Uncertainty: The Soul of Modeling, Probability & Statistics, a book which calls for a complete and fundamental change in the philosophy and practice of probability & statistics; author of two other books and dozens of works in fields of statistics, medicine, philosophy, meteorology and climatology, solar physics, and energy use appearing in both professional and popular outlets. Full CV (pdf updated rarely).
