Fooling Around With Fran
By Greg Glassman
This month we examine “Fran,” one of our benchmark workouts. The opportunity this affords for insights into human performance, programming, and ways of measuring and motivating progress is strong.
First and foremost, Fran is a couplet of barbell thrusters (front squat/push-press combo) and pull-ups. More specifically, her structure is 21 thrusters followed by 21 pull-ups, then 15 thrusters followed by 15 pull-ups and, finally, 9 thrusters followed by 9 pull-ups. We score the workout by time to completion. Our notation for this and other similar workouts is, “Three rounds, 21, 15 and 9 reps, for time, of 95-pound barbell thrusters and pull-ups.”
First exposure to this workout reveals Fran’s penchant for throwing a beating. Repeated exposures, where the goal is improved time, demonstrate a ferocity that speaks to the painful cost of elite fitness. Considering the thruster’s position as the most draining of all exercises and the pull-up’s reputation for winnowing athlete pools, there may be little surprise in Fran’s effects.
Coupled, the thruster and the pull-up work all major muscle groups, are perfectly complementary in that each contains exactly what the other lacks, and constitute three superfunctional core movements—the squat, push press and pull-up. But a closer analysis offers even greater appreciation and understanding of Fran’s character.
For any particular athlete, Fran represents a fixed amount of “work” in both the colloquial sense of work and in the more technical sense of work as a physicist would use the term. For the physicist, work is “the transference of energy that is produced by the motion of the point of application of a force and is measured by multiplying the force and the displacement of its point of application in the line of action.” In practical terms this means that we can measure work performed by multiplying an object’s weight by how high we lift it.
In the case of Fran we are performing 45 thrusters and 45 pull-ups in the course of the workout. Each thruster moves the same amount of weight the same distance, as does each pull-up. Measuring the work performed in lifting the bar alone is straightforward. We just multiply the bar’s weight by the distance each thruster rep takes the bar. But the work required to raise the bar is accompanied by the work required to raise the body for the squat and the arms overhead, and that’s just for the thruster. By adding the work required to lift the bar to the work required to squat and raise the arms overhead we can reasonably determine the work required of one thruster. Multiplying that total by 45 reps would yield the amount of work required to complete Fran’s thrusters. By measuring the work required of the pull-up and again multiplying by 45 reps we can determine the work required to complete Fran’s pull-ups. Adding the thruster total work to the pull-up total work gives us the total work required to complete Fran. For any athlete this value—the quantity of work—is fixed, regardless of capacity or performance.
But measuring the work required to squat and raise the hands overhead and to perform the pull-up is a bit nettlesome. We greatly simplified that task for the thruster movement by multiplying the travel of the center of mass, presumed to be between the athlete’s pubic bone and navel and in the frontal plane, by the weight of the athlete. We similarly approximated the work required to perform one pull-up by multiplying the travel of the center of mass by the athlete’s weight.
In the case of the squat to overhead thrust movement, much of the leg isn’t elevated the distance that the center of mass travels, and therefore our estimation of the work required to squat is high. Some of that is compensated for by the travel of the arms from start to finish, which exceeds the distance traveled by the center of mass.
It is the same in the case of the pull-up. Most of the arm isn’t elevated as much as the center of mass is, so our estimation of the work required to perform each pull-up will also be somewhat high. Because the arms are considerably lighter than the legs, we expect our overestimation of the pull-up’s work to be less than our overestimation of the work required to squat.
These measures derived from the travel of an athlete’s center of mass are less than ideal, but may still offer insight. While admitting that our methods are zero-order (we’ve not considered dynamics, for instance), we leave it to others more interested to refine our methods to make the same or other conclusions and leave them with noted physiologist Richard Burton’s offering that “the mechanics of human movement would seem to offer considerable scope for quantitative treatment involving muscle tensions and the arithmetic of levers. However, a simple limb movement may call on a number of muscles working together, and the relevant measurements may be hard to elicit, even from many shelves of anatomy books.”
If we take our measures from CrossFit athlete Greg Amundson, who is about 6 feet tall and weighs 200 pounds, we find that in the pull-up his center of mass travels 24 inches and in the thruster it travels 26 inches while the bar travels 47 inches.
From this data we calculate that each pull-up requires 400 foot-pounds of work and each thruster requires 805 foot-pounds of work—about 433 foot-pounds to move the body and 372 foot-pounds to move the load. Multiplying the sum of the work required to do one pull-up and one thruster by forty-five reps gives us the total work required to complete Fran—a whopping 54,225 foot-pounds of work. This figure is constant for Greg regardless of the time it takes him to complete Fran.
Already a couple of interesting things present themselves. First, the (unweighted) squat to overhead thrust and the pull-up are nearly equivalent in the amount of work required to complete a single rep. This was counterintuitive for the CrossFit staff. Second, with a 200-pound athlete, bodyweight accounts for about two-thirds of Fran’s demands. The first observation may offer programming ideas derived from the understanding that the squat and pull-up are metabolic equals. The second observation makes us curious about the performance potential of lighter vs. heavier athletes with Fran. After playing with the numbers we now believe that Fran selects for athletes lighter than 200 pounds.
While the amount of work required to complete Fran is constant for any given athlete, the average power, and therefore intensity, of the workout varies inversely with the time to completion. The faster the time, the greater the average power expressed throughout the workout—and power (intensity) is fundamental to the CrossFit creed. This encourages us to make some more calculations.
If we divide each of Greg’s last three efforts at Fran (his constant 54,225 foot-pounds of work) by the time to completion in seconds we find the average power for each effort in foot-pounds per second—a unit of power. These three efforts average 315 foot-pounds per second.
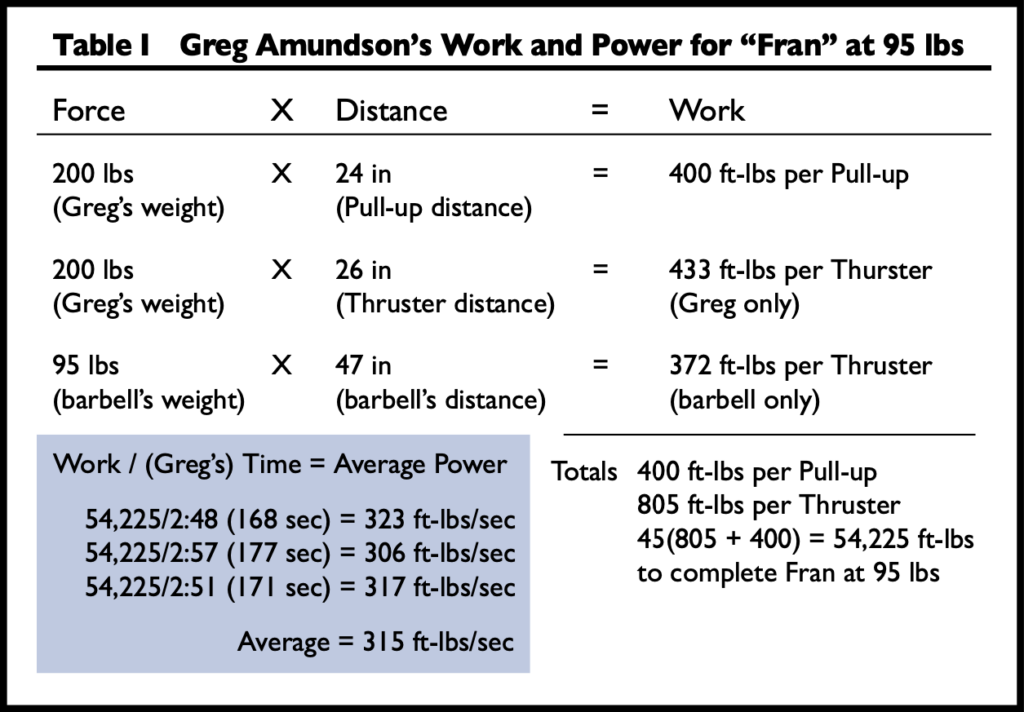
For comparison we had Greg perform a modified Fran with 115 pounds instead of the regular 95 pounds. This 20-pound increase in the barbell load brings the work required to complete Fran from 54,225 foot-pounds of work to 57,735 foot-pounds.
What did it do to Greg’s average power to complete this “Fat Fran”? It brought the average power down from 315 foot-pounds per second to 253 foot-pounds per second. This is a reduction in average power through the workout of nearly 20 percent.
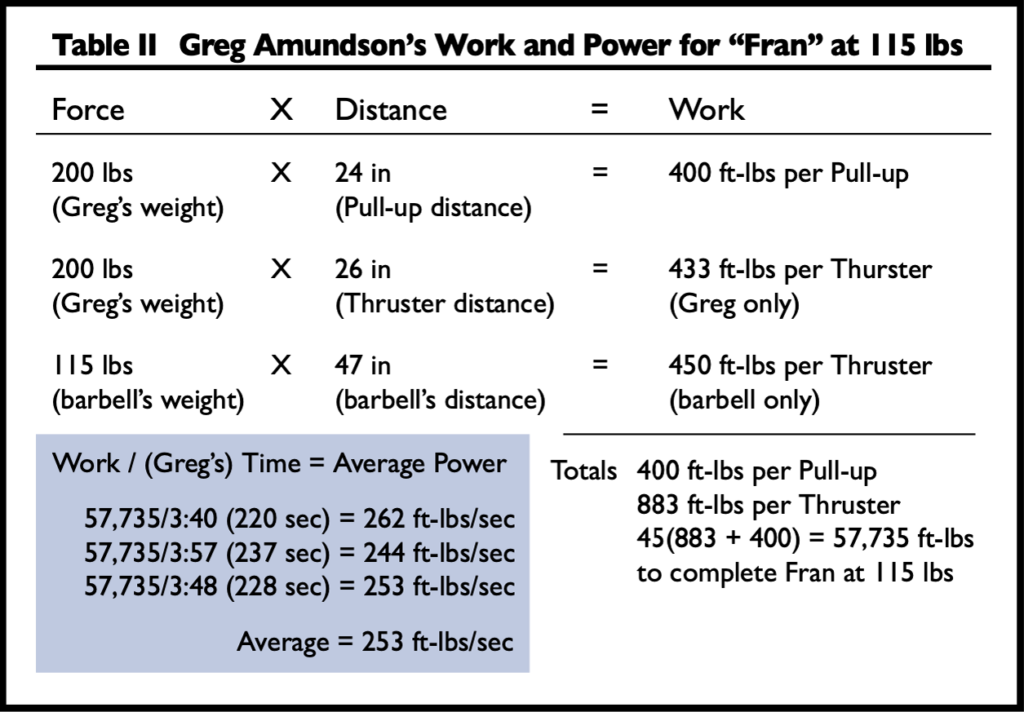
For comparison we had Greg also work one effort at a modified Fran with 75 pounds instead of the regular 95 pounds. This 20-pound decrease in the barbell load brings the work required to complete Fran from 54,225 foot-pounds to 50,715 foot-pounds.
What did it do to Greg’s average power to complete this “Anorexic Fran”? It brought the average power up from 315 foot-pounds per second to 338 foot-pounds per second. This is an increase in average power from the standard Fran of about 7 percent.
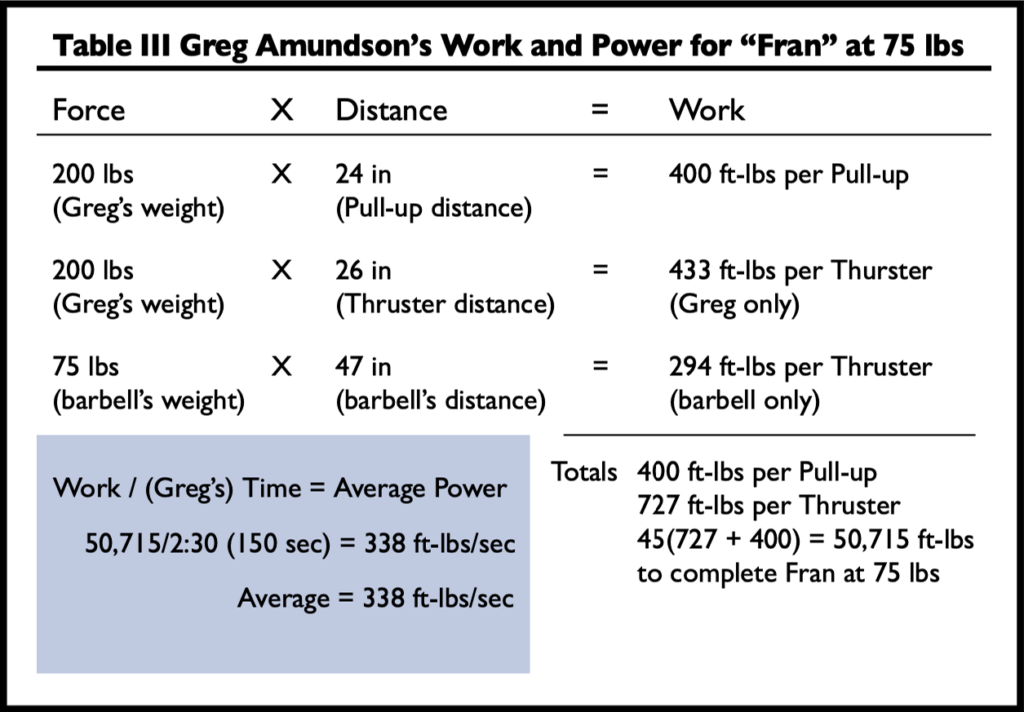
With a 75-pound load Greg completed the workout in 2:30. We know that Fran maximally compresses to about 2:20-2:25. That is the time required to complete Fran empty-handed, i.e., with no load on the thrusters and moving the arms simulating a pull-up. A further reduction in load would only decrease the power. Greg’s maximum power lies somewhere between 75 and 95 pounds.
More on Greg later. Let’s look at another family of variations on Fran where the load and reps are held constant. These variants are, borrowing a term from chemistry, “isomers” of Fran—variants where the parts are the same but the structure is different.
At rounds of 21, 15 and 9 repetitions of thrusters and pull-ups, Fran includes 45 thrusters and 45 pull-ups. What would happen to the time and consequently to the average power if Fran’s instructions were 45 thrusters at 95 pounds followed by 45 pull-ups?
One round of 45 thrusters and 45 pull-ups (1×45), three rounds of 15 thrusters followed by 15 pull-ups (3×15), 5 rounds of 9 thrusters and 9 pull-ups (5×9), and 9 rounds of 5 thrusters and 5 pull-ups (9×5) are exactly equivalent in mechanical work, yet very, very different in feel and effect. They will also return different times for any given athlete.
Looking at Fran’s isomers, the 45/45 split might seem to yield the fastest theoretical time because of the lack of transitions. The facts of muscle strength and stamina will, however, exert a dominating influence in all but the strongest athletes.
In the 9×5 split the transitions are numerous but they provide relief—8 breaks of effort type rather than one. This would allow someone with muscular weakness in the thruster and pull-up to shift efforts before bogging down or stalling. For athletes having trouble with fewer splits, the 9×5 split may keep them moving but might also bring the cardiorespiratory demands through the roof because any work is harder than resting.
Our expectation is that, generally, times for the different splits would rank, quickest to slowest, 9×5, 5×9, 3×15 and 1×45. The 21/15/9 split of Fran will, for most people, likely come between 3×15 and 1×45.
If this has suggested a continuum, applicable to most athletes, from strength to metabolic wallop based on degree of fracture in the couplet, you’re seeing what we are seeing. The less fractured isomer, 1×45, is more demanding of strength and stamina than the more fractured isomer of 9×5.
As athletes develop in CrossFitting, we would expect their best times to move from the 9×5 side of the continuum to the 1×45 side as their strength, stamina and metabolic conditioning advance. The advantage of the more fractured split should disappear with continued athletic development. An athlete rests to recover from weakness—whether metabolic or muscular.
Back to Greg. How might Greg Amundson best his Fran time of 2:48? Here’s what we see. When he goes a little lighter (20 pounds), his power goes up 7 percent and won’t be further increased by going lighter. When he goes a little heavier (20 pounds), his power drops 20 percent. We would predict that spending more time with Fran’s heavier sisters would be the most efficacious route to Greg’s improved performance. Improving Greg’s Fran is not our goal, however, and neither is analysis. But analysis opens our minds and more importantly opens our eyes. We cannot yet derive fundamental principles more valuable than measure, think and experiment. The better part of measurement may lie in knowing what we are doing, so that we can do something different.
This article, by BSI’s co-founder, was originally published in The CrossFit Journal. While Greg Glassman no longer owns CrossFit Inc., his writings and ideas revolutionized the world of fitness, and are reproduced here.
Coach Glassman named his training methodology ‘CrossFit,’ which became a trademarked term owned by CrossFit Inc. In order to preserve his writings in their original form, references to ‘CrossFit’ remain in this article.
